How To Find Surface Area Of A Right Triangular Prism

Triangular Prism Shape

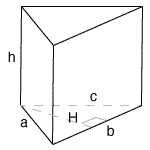
Triangular Prism Diagram with h = height and side lengths a, b and c

a = side length a
b = side length b = bottom triangle base of operations b
c = side length c
h = height of prism
H = height of lesser triangle
Five = volume
A_tot = total surface surface area = all sides
A_lat = lateral surface surface area = all rectangular sides
A_peak = top surface area = summit triangle
A_bot = lesser surface area = lesser triangle

A triangular prism is a geometric solid shape with a triangle as its base. It'southward a iii-sided prism where the base of operations and top are equal triangles and the remaining 3 sides are rectangles.

Figurer Use

This calculator finds the book, surface expanse and summit of a triangular prism. Surface area calculations include elevation, bottom, lateral sides and full expanse. Elevation is calculated from known book or lateral surface area.

Units: Units are shown for convenience only do not affect calculations. Answers will be the same whether in feet, ftⁱⁱ, ft^three, or meters, m², thou³, or whatsoever other unit of measurement measure out.

Meaning Figures: Choose the number of significant figures or leave on motorcar to permit the computer determine number precision.

Triangular Prism Formulas in terms of meridian and triangle side lengths a, b and c:

Book of a Triangular Prism Formula

Finds the 3-dimensional space occupied by a triangular prism.

\[ V = \dfrac{i}{4}h \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ V = \dfrac{1}{4}h \sqrt{(c+a-b)(a+b-c)} \\\times \sqrt{(a+b+c)(b+c-a)} \]

Top Expanse of a Triangular Prism Formula

Finds the area contained by the triangular surface at the peak of the prism. This is the aforementioned expanse as the bottom surface area.

\[ A_{top} = \dfrac{ane}{iv} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ A_{meridian} = \dfrac{1}{four} \sqrt{\begin{aligned}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c)\end{aligned}} \]

Bottom Expanse of a Triangular Prism Formula

Finds the area independent by the triangular surface at the lesser of the prism. This is the same area as the acme surface expanse.

\[ A_{bot} = \dfrac{one}{four} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ A_{bot} = \dfrac{1}{4} \sqrt{\begin{aligned}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c)\end{aligned}} \]

Lateral Surface Area of a Triangular Prism Formula

Finds the total area contained by the iii rectangular sides of the prism. You tin call back of the lateral surface expanse as the full surface area of the prism minus the two triangular areas at the height and bottom of the prism.

\[ A_{lat} = h (a+b+c) \]

Total Surface Area of a Triangular Prism Formula

Finds the total area of all sides of a triangular prism. Total surface area of a prism includes the area of the superlative and bottom triangle sides of the prism, plus the surface area of all 3 rectangular sides.

\[ A_{tot} = A_{summit} + A_{bot} + A_{lat} \]

Pinnacle of a Triangular Prism Formula in Terms of Volume

Finds the peak of a triangular prism by solving the Book Formula for superlative. Height, h, is calculated from volume, V, and side lengths a, b and c.

\[ h = \dfrac{4V}{\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} \]

\[ h = 4V \div \left[ \, \sqrt{(c+a-b)(a+b-c)} \\\times \sqrt{(a+b+c)(b+c-a)} \, \correct] \]

Top of a Triangular Prism Formula in Terms of Lateral Expanse

Finds the height of a triangular prism past solving the Lateral Surface Surface area Formula for pinnacle. Elevation, h, is calculated from lateral surface expanse, A_lat, and side lengths a, b and c.

\[ h = \dfrac{A_{lat}}{(a+b+c)} \]