How To Find N Terms In Arithmetic Progression

Sum of n Terms of an AP

An arithmetic progression is a sequence of numbers or variables in which the divergence between consecutive terms is the same. There can exist an space number of terms in an AP. To find the sum of n terms of an AP, we use a formula start founded by Johann Carl Friedrich Gauss in the 19th century. Let us larn all most the sum of due north terms of an AP in this article.

1.	What is Sum of n Terms of an AP?
2.	Sum of north Terms of AP Formula
3.	Sum of n Terms of AP Proof
4.	Sum of AP Formula for an Space AP
5.	FAQs on Sum of north Terms of an AP

What is Sum of n Terms of an AP?

In the 19th century in Federal republic of germany, a Math class for class 10 was going on. The teacher asked her students to sum all the numbers from 1 upward to 100. The students were struggling to summate the sum of all these numbers. One boy shouted out the reply 5050 while the other students were even so in the initial steps of calculating the sum. This boy was the bully German mathematician Carl Friedrich Gauss. How did he arrive at the sum then quickly?

Well, he noticed that terms equidistant from the beginning and the end of the serial had a abiding sum equal to 101.

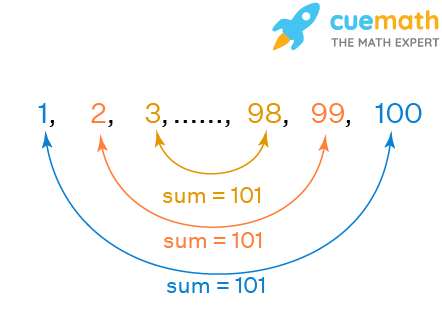
sum of first n terms of an AP

We can see that in sequence 1, ii, 3, ..., 100, there are fifty such pairs whose sum is 101. Thus, the sum of all terms of this sequence is fifty × 101 = 5050.

Sum of n Terms of AP Formula

The sum of n terms of an AP can be easily found out using a uncomplicated formula which says that, if we have an AP whose first term is a and the common departure is d, then the formula of the sum of n terms of the AP is S_{due north} = n/2 [2a + (n-ane)d].

In other words, the formula for finding the sum of kickoff due north terms of an AP given in the course of "a, a+d, a+2nd, a+3d, ....., a+(north-1)d" is:

Sum = north/2 × [2a + (n-1)d]

Now, allow us talk over one more case for the sum of n terms of an AP formula, which is "What volition exist the formula of the sum of northward terms in AP when the last term of the progression is given?".

Sum of n Terms in AP when Last Term is Given

The sum of the first n terms of an arithmetic progression when the nth term, a_n is known is:

S_n=due north/2 × [a_i+a_n]

Sum of north Terms of AP Proof

In this department, we are going to learn the proof of sum of n terms of an AP formula. Permit us consider the arithmetic progression with n terms:

a, a+d, a+2d,... (a+(n−2)d), (a+(n−1)d)

The sum of due north terms of this progression is:

S_n =a + (a+d) + … + (a+(n−2)d) + (a+(n−one)d) → (1)

Past reversing the order of the terms of this equation:

S_n = (a+(north−i)d) + (a+(northward−two)d) + … + (a+d) + a → (2)

We see that the sum of corresponding terms of equation (1) and equation (2) yield the same sum which is 2a+(n−1)d. Nosotros know that in that location are totally n terms in the above AP. So by adding (1) and (2), we get:

sum of n terms of an ap proof

2S_n = northward(2a+(n−1)d)

Southward_n = n/2 (2a+(n−1)d)

The to a higher place sum of arithmetic progression equation can be written as:

Due south_northward = n/2 (2a+(northward−1)d)

S_n = n/2 (a+a+(n−i)d)

Sn = n/2 (a₁+a_n) [∵ a_n = a+(n−1)d and a = a_ane]

Thus, the sum of arithmetic progression equations are:

S_north = n/2 (2a+(n−1)d), or,

Southward_northward = n/two (a₁ + a_north)

Let's take a look at the post-obit flowchart to get an idea of the formula that has to exist used to find the sum of arithmetic progression according to the information available to us.

sum of n terms of an AP formula

Sum of AP Formula for an Infinite AP

Let us consider an example for the sum of an infinite AP.

2 + 5 + 8 + ...

Here, the outset term is a = 2. The common difference is d = 3. The number of terms is, n = ∞. Substitute all these values in sum of AP formula:

Due south_northward = due north/2 (2a+(n−ane)d)

S_north = ∞/2 (two(2)+(∞−i)3)

S_n= ∞

We plant the sum of infinite AP to exist ∞ when d > 0. In the same way, the sum of infinite AP is −∞ when d < 0.

Thus, \(\text { Sum of space } A P=\left\{\begin{array}{ll}
\infty, & \text { if } \quad d>0 \\[0.3cm]
-\infty, & \text { if } \quad d<0
\cease{array}\right.
\)

Sum of northward Terms of AP Tips and Tricks:

The sum of arithmetics progression whose offset term is a and the mutual difference is d tin can exist calculated using 1 of the post-obit formulas: S_northward = due north/2 (2a+(n−1)d) and S_north = due north/2 (a_i+a_northward).
The sum of AP of n natural numbers is north(n+1)/2.

Challenging Questions:

Find the sum: 115, 112, 110,…, to 13 terms.
How many terms of the AP nine, 17, 25, ... must be taken to give a sum of 636?

☛ Related Topics:

Sum of north Terms of an AP Estimator
nth Term of an AP
Arithmetic Sequence Estimator

Sum of north Terms in AP Examples

Instance ane: Calculate the sum of the first xx terms of the following AP: S = 190 + 167 + 144 + 121 + …

Solution:

Using the sum of n terms of an AP formula,

Southward = due north/2 (2a+(n−1)d).

Here, we have a = 190, d = −23, and n = twenty. Substituting all these values in the above formula,

Southward = 20/2 (ii(190)+(20−1)(−23))

=10 (380−437)

= x(−57)

= −570

Respond: Therefore, the sum of the first 20 terms of the given AP is - 570.
Example 2: Consider the following AP: 24, 21, 18, … How many terms of this AP must exist considered then that their sum is 78?

Solution:

Permit the number of terms that requite the sum 78 be denoted as n. We have a = 24, d = −3, and South = 78. Substituting all these values in the sum of northward terms of an AP formula,

S = n/2 (2a+(n−1)d)

⇒ 78 = n/2 (48−three(north−ane))

⇒ 78 = n/two (51−3n)

⇒ 3n² − 51n + 156 = 0

⇒ n² −17n + 52 = 0

⇒ (n−four)(n−thirteen) = 0

⇒ north = 4, xiii

Answer: Therefore, the sum of either 4 terms or 13 terms of the given AP is 78.
Instance 3: Given a = v, d = three, and a_n = 50, find the value of South_n.

Solution:

The given values are a = 5 = a₁, d=3, and a_n=50. We know that the nth term of AP is given by the formula a_north = a+(n−1)d.

⇒ 50 = 5+(north−one)iii

l = 5+3n−3

50 = 3n+2

48 = 3n

xvi = n

By using the sum of AP formula,

S_northward = n/2 (a₁+a_n)

Southward_n = 16/2 (five+50)

Due south_n = 8(55)

S_n = 440

Respond: Therefore, the value of South_n is 440.

go to slidego to slidego to slide

Want to build a potent foundation in Math?

Become across memorizing formulas and understand the 'why' backside them. Feel Cuemath and get started.

Book a Costless Trial Form

Practice Questions on Sum of n Terms of an AP

become to slidego to slide

FAQs on Sum of due north Terms of an AP

What is the Sum of n Terms of an AP Formula?

The sum of north terms of an AP can be found using one of the following formulas:

S_n = northward/2 (2a+(n−1)d)
Southward_n = n/2 (a₁+a_n)

Hither, a = a₁ = the first term, d = the common difference, n = number of terms, a_north = north^thursday term, S_n = the sum of the kickoff northward terms.

What is the Unremarkably Used Sum of AP Formula?

The formula to find the sum of n terms in AP is Due south_{due north} = n/2 (2a+(n−1)d), in which a = first term, northward = number of terms, and d = common difference between sequent terms.

What is the Sum of First n Terms of an AP: a, 3a, 5a ...?

The given AP is a, 3a, 5a, ... The first term is a and the common departure is 2a. The sum of n terms of the given AP is S_n = north/2 (2a+(n−i)2a).

⇒ S_n = n/2 (2a + 2an - 2a)

⇒ S_n = due north/two (2an)

⇒ Southward_n = an^two

The sum of northward terms of AP a, 3a, 5a, ... is an².

What is the Sum of an Arithmetics Sequence?

The sum of an arithmetic sequence is the sum of all the terms in information technology. Nosotros apply the first term (a), the common difference (d), and the full number of terms (due north) in the AP to find its sum. The formula used to find the sum of due north terms of an arithmetic sequence is n/two (2a+(due north−i)d).

What is the Sum of n Terms of an AP when the Final Term is Given?

If a_n is the n^th term of an arithmetic progression, a is the starting time term, and north is the total number of terms, then we tin can use the following formula to observe its sum: S_n = n/2 (a_one+a_northward).

Source: https://www.cuemath.com/algebra/sum-of-n-terms-of-an-ap/

Posted by: buchanmusur1997.blogspot.com